Introduction
Yes, let us not give freedom to the tokens! Let the experts choose the tokens! This isn’t politics we’re talking about here. I’m actually referring to the how Mixture-of-Experts by Expert Choice Routing1 works conceptually.
In this quick entry I would like to implement the Expert Choice Routing method in PyTorch based on translated Jax code from the Flaxformers archive. The Flaxformers implementation is particularly easy to understand and is easily ported to PyTorch. There are limitations of course since Jax uses a very different method for launching distributed training, but the routing is really crux of MoE. We can address distributed training when we work through incorporating the routing scheme in a MoE layer of a transformer.
Expert Choice Routing Explained
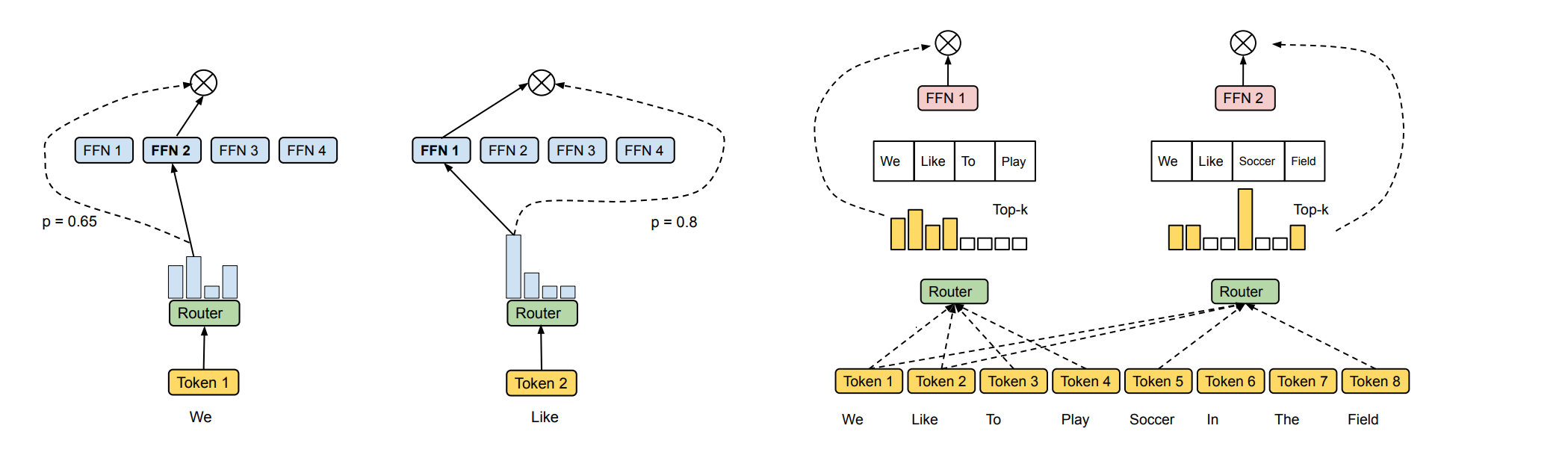
As presented in the above figure you can see conventional routing and expert choice on the right. Immediately it becomes clear that there is crossover between which tokens will be routed to FFN1 and FFN2. In Expert Choice unlike other conventional schemes which map individual tokens to a single router experts can choose a variable number of routers. This is because we can use the routing probabilities to weight the contribution of computed outputs from multiple experts.
We can get a similar effect when tokens choose the router they use for computation (think switch transformer2), but we would have to make all the experts participate and would lose sparsity by doing so and thus we would use more FLOPs. Expert Choice allows us to tune the total FLOPs by changing the capacity factor c. When the capacity factor is 1.0 computation is equally distributed among experts for each token. When the capacity factor falls below 1.0, computation is still evenly distributed but each token is not treated equally and may experience less influence from experts.
The authors of the paper explain how this mechanism works more concretely:
Different from conventional routing, an expert choice method independently selects top-k tokens for each expert, where k is a fixed expert capacity (i.e. the number of tokens each expert can take). Despite its simplicity, expert choice achieves perfect load balancing by design. It also enables more flexible allocation of model compute since tokens can be received by a variable number of experts.
In our experiments, we set k as:
where n is the total number of tokens in the input batch (such as batch size × sequence length), c is the capacity factor, and e is the number of experts. The capacity factor c denotes on average how many experts are utilized by a token. Given input token representations where d is the model hidden dimension, our method produces a token-to-expert assignment denoted by three output matrices I, G and P. The matrix I is an index matrix where specifies j-th selected token of the i-th expert. The gating matrix denotes the weight of expert for the selected token, and refers to an one-hot version of that will be used to gather tokens for each expert. These matrices are computed using a gating function,
where S denotes the token-to-expert affinity scores, denotes the expert embeddings, and TopK() selects the k largest entries for each row of .
Implementation
Essentially, input tokens are taken in from the previous layer and projected via the and activation. Using the highest probabilities and their indices are returned. Using these probabilities and their indices we form two new tensors. First we form what is referred to as the dispatch_mask via the gating indices which decides what tokens will be processed by what experts. We also form a combine_weights tensor which provides the contribution of each each expert’s output that will be combined (reduced) when all outputs are assembled from each expert.
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.distributed as dist
# mixed precision support
from torch.cuda.amp import autocast
from typing import List, Optional
def get_expert_capacity(num_tokens, capacity_factor, num_experts):
return int(round(num_tokens * capacity_factor / num_experts))
class ExpertChoiceRouter(nn.Module):
def __init__(self, embed_dim, num_experts, capacity_factor=1.0):
super(ExpertChoiceRouter, self).__init__()
self.embed_dim = embed_dim
self.num_experts = num_experts
self.capacity_factor = capacity_factor
self.gate = nn.Linear(embed_dim, num_experts)
self._init_weights()
def _init_weights(self):
nn.init.normal_(self.weight, std=2e-2)
if self.bias is not None:
nn.init.constant_(self.bias, 0.0)
def forward(self, x) -> torch.Tensor:
"""
Args:
x: (batch_size, seq_len, embed_dim)
Returns:
dispatch_mask: (batch_size, num_tokens, num_experts, expert_capacity)
combine_weights: (batch_size, num_tokens, num_experts, expert_capacity)
"""
with autocast(enabled=False):
gate_logits = self.gate(x)
gate_probs = F.softmax(gate_logits, dim=-1)
dispatch_mask, combine_weights = self.calculate_routing_parameters(
gate_probs
)
return dispatch_mask, combine_weights
def calculate_routing_parameters(
self, gate_probs: torch.Tensor
) -> List[torch.Tensor, torch.Tensor]:
"""
Args:
gate_probs: (batch_size, seq_len, num_experts)
Returns:
dispatch_mask: (batch_size, num_tokens, num_experts, expert_capacity)
combine_weights: (batch_size, num_tokens, num_experts, expert_capacity)
"""
num_tokens = gate_probs.shape[1]
# Calculate expert capacity for topk calculation
expert_capacity = get_expert_capacity(
num_tokens, self.capacity_factor, self.num_experts
)
# Calculate the topk router probabilities and corresponding
# token indices for each token in each batch
# shape: (batch_size, num_experts, expert_capacity)
expert_gate, expert_index = torch.topk(gate_probs, k=expert_capacity, dim=-1)
# Create a mask for the expert dispatch
# shape: (batch_size, num_experts, expert_capacity, num_tokens)
dispatch_mask = F.one_hot(expert_index, num_classes=num_tokens).to(torch.int32)
# shape: (batch_size, num_tokens, num_experts, expert_capacity)
dispatch_mask = dispatch_mask.permute(0, 3, 1, 2)
# Multiply the expert gate probabilities with the dispatch mask elementwise
combine_weights = torch.einsum(
"... e c, ... n e c -> ... n e c", expert_gate, dispatch_mask.float()
)
return dispatch_mask, combine_weightsAs I already expressed earlier things get a bit trickier once we’re done with routing. Now, we need to deal with how experts themselves are handled during distributed training. In Jax there exists the ability to map computation onto multiple devices by mapping a function via pmap. In PyTorch we do not have an abstraction to map to multiple devices in the same manner. When we send inputs to each expert we need to be conscious of how PyTorch Distributed works, and to play nicely with it. Nowadays there are basically two main distributed implementations: Distributed Data Parallel (DDP) and Fully Sharded Data Parallel (FSDP). The difference in these implementations is how model weights are broken up among available GPUs and how they are aggregated during backpropagation. We want our code to work with both distributed implementations. Note to future self: I really should write an entry on distributed computing in PyTorch.
When implementing the MoE layer used for routing and doing computation in each expert, I took inspiration from DeepSeekv2’s3 implementation of MoE. This basically assumes at a minimum that every expert will reside on it’s only device. If we increase the number of devices in each process group, then we will essentially increasing the number of expert replicates (expert with the same weights processing different tokens). This can be dealt with in PyTorch by ensuring that the world size is evenly divisible by the number of experts and that process groups for each expert were created.
Instead of performing multiplication with the dispatch_mask in the MoELayer, I distributed that computation among the experts using an ExpertWrapper class. This also applies to the use of the combine_weights tensor as well. Notice that these multiplications are element-wise without reduction. We leave the final summation of outputs to the forward method of the MoELayer.
class ExpertWrapper(nn.Module):
"""Moves the expert on to certain process group"""
def __init__(self, expert: nn.Module):
super(ExpertWrapper, self).__init__()
self.expert = expert
def forward(
self,
x: torch.Tensor,
dispatch_mask: torch.Tensor,
combine_weights: torch.Tensor,
):
"""
Args:
x: (batch_size, seq_len, embed_dim)
dispatch_mask: (batch_size, num_tokens, expert_capacity)
combine_weights: (batch_size, num_tokens, expert_capacity)
Returns:
expert_output: (batch_size, seq_len, embed_dim)
"""
expert_inputs = torch.einsum(
"b n ..., b n c -> b c ...", x, dispatch_mask.float()
)
expert_outputs = self.expert(expert_inputs)
combined_outputs = torch.einsum(
"b c ..., b n c -> b n ...", expert_outputs, combine_weights
)
return combined_outputs
class MoELayer(nn.Module):
def __init__(
self,
embed_dim,
num_experts: int,
process_size: Optional[int] = None,
expert: nn.Module = None,
):
super(MoELayer, self).__init__()
self.embed_dim = embed_dim
self.num_experts = num_experts
if process_size is not None:
assert process_size == dist.get_world_size()
self.num_replicates = self.num_experts // process_size
self.process_rank = dist.get_rank()
self.experts = nn.ModuleList(
[
(
ExpertWrapper(expert=expert)
if i > self.process_rank * self.num_replicates
and i < (self.process_rank + 1) * self.num_replicates
else None
)
for i in range(self.num_experts)
]
)
else:
self.num_replicates = 1
self.process_rank = 0
self.experts = nn.ModuleList([ExpertWrapper(expert) for _ in range(num_experts)])
self.router = ExpertChoiceRouter(embed_dim, num_experts)
def forward(self, x: torch.Tensor) -> torch.Tensor:
"""
Args:
x: (batch_size, seq_len, embed_dim)
Returns:
expert_output: (batch_size, seq_len, embed_dim)
"""
dispatch_mask, combine_weights = self.router(x)
expert_outputs = []
for i, expert in enumerate(self.experts):
if expert is not None:
expert_outputs.append(expert(x, dispatch_mask[:, :, i], combine_weights[:, :, i]))
expert_output = torch.sum(torch.stack(expert_outputs, dim=2), dim=2)
return expert_outputThe MoELayer class and ExpertWrapper can together be substituted for naive MLP layers in a transformer-based model by simply wrapping your MLP class with the ExpertWrapper and then subsequent initialization in the MoELayer class. Care must be taken when wrapping modules with DDP or FSDP, and it would be helpful to review PyTorch documentation before doing so.
Wrapping Up
I have explained how Mixture-of-Experts by Expert Choice Routing1 works both conceptually and in depth with working code. When I looked around online I couldn’t find a decent open-source PyTorch implementation so I created my own. Expert Choice Routing has become a foundation on which several new extensions have been built. Please check out my entry on MoNE, Should I moan? for further details.