Overview
Well, I’m not one to MoNE1 even when a research paper is an incremental nudge in the direction of improvement. Mixture of Nested Experts is conceptually quite interesting. By using modified expert choice routing, groups of neurons (experts) can choose what tokens will be involved in computation in both self-attention and in the feedforward layers. In practice, performance should be roughly equivalent to an equivalently sized network without any version of sparsity. This paper builds upon a body of research from Google; namely MOE with Expert Choice Routing2, Mixture-of-Depths3, and MatFormer4. We will see that combining these ideas leads to significantly better performance than either MatFormer or Mixture-of-Depths.
When I say neurons in this case I mean the fractions of the embedding dimension with which we project our hidden states. This means for a given model we can activate a given fraction of parameters in each layer. From a resource perspective this means expert groups can select how many tokens will be involved in computation and in aggregate this should result in less compute based on how many tokens are allocated to a given fraction of parameters. I need to note that this is not fully dynamic in that groups of parameters are set before training begins in a way similar to MatFormer4
Methodology
The models evaluated in this paper are limited to vision related modalities of images and video. This probably was done to stay consistent with MatFormer and to deal with additional complexity when dealing with causal inference (as was dealt with in Mixture-of-Experts).
 In terms of the structure the MoNE model the authors only make modification to the self-attention blocks preserving the overall structure of standard ViT. This is nice since it does make it easier to compare with the baseline ViT.
In terms of the structure the MoNE model the authors only make modification to the self-attention blocks preserving the overall structure of standard ViT. This is nice since it does make it easier to compare with the baseline ViT.
In the figure above taken from the MoNE paper, we can see a fractional components that make up a part of MatFormer (a). Extending this idea by adding conditional computation via routing based on Expert Choice, tokens are now chosen by groups of experts via a Expert Preferred Routing. This is essentially the same as Expert Choice except now the TopK token selection is performed for each expert as opposed to evenly distributing tokens across all experts. I provide examples of Expert Choice routing and make the previous modification described above to realize this Expert Preferred Routing.
In terms of the expert capacity we see something that diverges from previous methodologies. In the case of MoNE1 the authors use sequential least squares programming optimization (SLSQP). This is fortunately readily available in SciPy and can be implemented in Python quite easily. SLSQP is an iterative method for solving constrained nonlinear optimization problems and is the default when using SciPy for constrained optimization problems.
Implementation
The main idea in this paper is apply routing to fractions of weights (or equivalently groups of neurons). The routing method as described earlier is Expert Preferred Routing. In an effort to experiment with Mixture-of-Depths3 (MoD) on my own I wrote up code for both the routing and use in the model with optional MOE functionality. The routing in the case of MoD is Expert Choice, and with some simple modifications we can realize Expert Preferred Routing.
import numpy as np
from scipy.optimize import minimize
def optimize_capacity(E: int, e_c: float, delta: float = 2, beta: float = 10) -> np.ndarray:
"""
Optimize the capacity distribution across experts using SLSQP optimization.
Args:
E (int): Number of experts.
e_c (float): Target effective capacity (0 < e_c < 1).
delta (float): Parameter to incentivize usage of larger models (δ > 1). Default is 2.
beta (float): Parameter to control the entropy term (β > 0). Default is 10.
Returns:
np.ndarray: Optimal capacity distribution across experts.
"""
def objective(c: np.ndarray) -> float:
return -np.sum(c * delta**np.arange(E)) + beta * np.sum(c * np.log(c))
def constraint_sum_to_one(c: np.ndarray) -> float:
return np.sum(c) - 1
def constraint_effective_capacity(c: np.ndarray) -> float:
return np.sum(c * 2**(E - 1 - np.arange(E))) - e_c
c0 = np.ones(E) / E
bounds = [(0, 1) for _ in range(E)]
constraints = [
{'type': 'eq', 'fun': constraint_sum_to_one},
{'type': 'eq', 'fun': constraint_effective_capacity}
]
result = minimize(
objective,
c0,
method='SLSQP',
bounds=bounds,
constraints=constraints
)
return result.xIf we assume we have 4 experts we arrive at an optimal capacity distribution:
| Expert | Capacity |
|---|---|
| C₁ | 24.43% |
| C₂ | 17.64% |
| C₃ | 20.79% |
| C₄ | 37.15% |
given the following parameters:
Now that we can calculate the optimal capacity for each expert, we can implement the routing mechanism. The authors provide the following figure for how the routing mechanism works.
My implementation of the Preferred Routing mechanism is basically a modification of the Expert Choice routing mechanism. The only real difference is that we now have a TopK token selection for each expert as opposed to evenly distributing tokens across all experts. In order to avoid creating multiple dispatch masks for each expert we can set a maximum capacity. The original Expert Choice implementation was borrowed from the Flaxformer library5.
class ExpertsPreferredMaskedRouter(MaskedRouter):
"""
Masked matmul router using expert-preferred token assignment with variable capacities.
This router is similar to ExpertsChooseMaskedRouter but allows for different capacities
for each expert. Experts choose tokens in order, with each expert selecting up to its
specified capacity.
Attributes:
router_weights: Configurable module used to compute router logits from token inputs.
jitter_noise: Amplitude of jitter noise applied to router logits.
dtype: Numeric float type for returned combine array. All actual computations
are performed in float32 of the input for stability.
ignore_padding_tokens: Whether to ignore padding tokens during routing.
"""
def __init__(
self,
router_weights: nn.Linear,
jitter_noise: float,
ignore_padding_tokens: bool,
dtype: Optional[torch.dtype] = None,
):
super().__init__(
router_weights, jitter_noise, ignore_padding_tokens, dtype=dtype
)
def _compute_routing_instructions(
self,
router_probs: torch.Tensor,
expert_capacities: List[int],
padding_mask: Optional[torch.Tensor] = None,
) -> RouterMask:
"""
Compute routing instructions based on router probabilities and expert capacities.
Args:
router_probs: Router probabilities.
Shape: [num_groups, tokens_per_group, num_experts]
expert_capacities: List of capacities for each expert.
padding_mask: Optional boolean tensor indicating which tokens are padding.
Shape: [num_groups, tokens_per_group]
Returns:
Dispatch and combine arrays for routing with masked matmuls.
"""
num_groups, tokens_per_group, num_experts = router_probs.shape
device = router_probs.device
assert len(expert_capacities) == num_experts, "Number of expert capacities must match number of experts"
if padding_mask is not None:
router_probs = router_probs * padding_mask.unsqueeze(-1)
max_capacity = max(expert_capacities)
dispatch_mask = torch.zeros(
(num_groups, tokens_per_group, num_experts, max_capacity),
dtype=torch.int32,
device=device,
)
combine_array = torch.zeros_like(dispatch_mask, dtype=self.dtype)
# Transpose router_probs for each group
router_probs_t = router_probs.transpose(1, 2)
for expert_idx, capacity in enumerate(expert_capacities):
expert_probs = router_probs_t[:, expert_idx, :]
available_mask = (dispatch_mask.sum(dim=(2, 3)) == 0).float()
masked_probs = expert_probs * available_mask
expert_gate, expert_index = torch.topk(masked_probs, k=capacity, dim=-1)
# Update dispatch mask
dispatch_mask[torch.arange(num_groups).unsqueeze(1), expert_index, expert_idx, torch.arange(capacity)] = 1
# Update combine array
combine_array[torch.arange(num_groups).unsqueeze(1), expert_index, expert_idx, torch.arange(capacity)] = expert_gate
# Reshape dispatch mask and combine array to match expected output shape
dispatch_mask = dispatch_mask.permute(0, 1, 2, 3)
combine_array = combine_array.permute(0, 1, 2, 3)
# Calculate auxiliary loss (you may want to implement a custom loss for this router)
auxiliary_loss = torch.tensor(0.0, device=device, dtype=self.dtype)
return RouterMask(dispatch_mask, combine_array, auxiliary_loss)
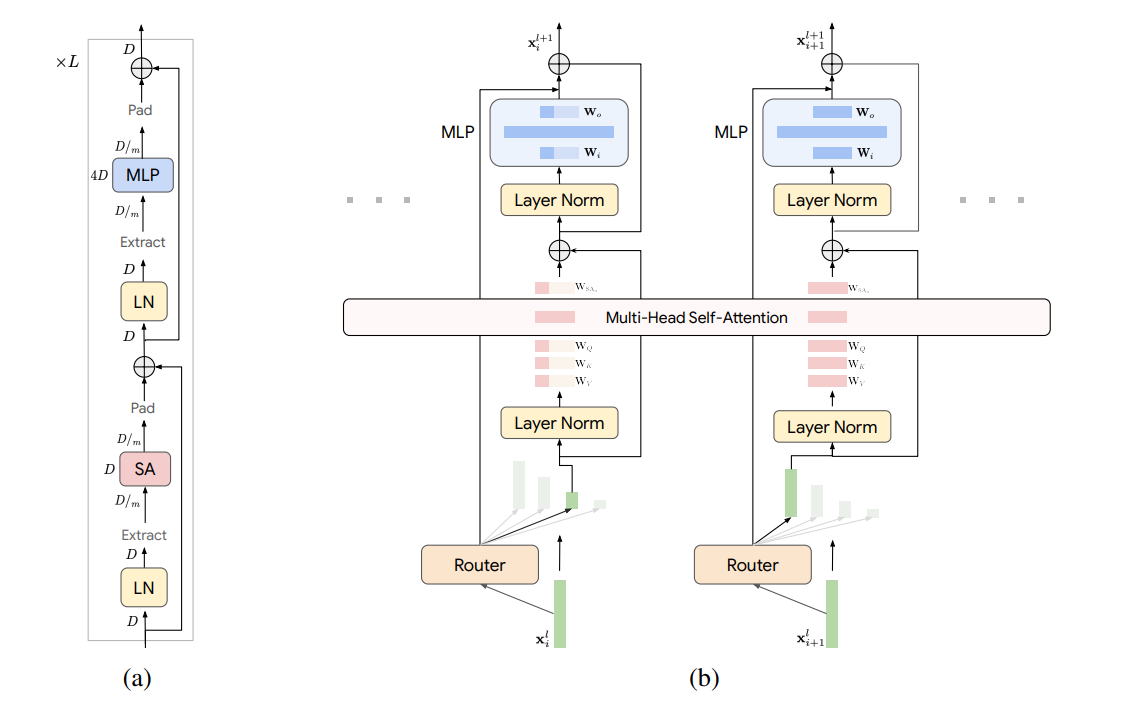
Now that we have the routing mechanism we can implement the MoNE model. Unlike typical transformer blocks which do not deal with dynamic routing of nested experts, we have to make some special considerations about how we project our inputs in the attention and feedforward layers. We can use the dispatch mask creatively to break apart our input and aggregate it ensuring that tokens are in the proper order prior to attention and feedforward computation. The authors provide the following figure for the overall structure of the model.
We can abstract the projection of nested experts by creating a custom linear layer that works with dispatched tokens. This allows us to re-use the same class multiple times within an attention block. This also keeps the code relatively modular and preserves the same structure of a standard transformer block. We do have to keep in mind however that the tensor passed between functions is changing shape in order to implement the nesting of experts. The custom linear layer is implemented as follows:
class NestedLinear(nn.Linear):
"""
A nested linear layer that applies different fractions of weights to different experts.
Args:
in_features (int): Size of each input sample.
out_features (int): Size of each output sample.
num_experts (int): Number of experts.
nested_forward (bool): Whether to use nested forward pass. Default: True.
combine_output (bool): Whether to combine expert outputs. Default: True.
"""
def __init__(
self,
in_features: int,
out_features: int,
num_experts: int,
nested_forward: bool = True,
combine_output: bool = True,
):
super().__init__(in_features, out_features)
self.in_features = in_features
self.out_features = out_features
self.num_experts = num_experts
self.nested_forward = nested_forward
self.combine_output = combine_output
# Custom initialization
self.reset_parameters()
def reset_parameters(self) -> None:
# Initialize the entire weight matrix
nn.init.kaiming_uniform_(self.weight, a=math.sqrt(5))
# Adjust the initialization for nested experts
if self.nested_forward:
for i in range(self.num_experts):
dim_slice = self.in_features // (2 ** i)
std = math.sqrt(2.0 / (dim_slice + self.out_features))
nn.init.normal_(self.weight[:, :dim_slice], mean=0.0, std=std)
if self.bias is not None:
fan_in, _ = nn.init._calculate_fan_in_and_fan_out(self.weight)
bound = 1 / math.sqrt(fan_in) if fan_in > 0 else 0
nn.init.uniform_(self.bias, -bound, bound)
def forward(self, x: torch.Tensor, dispatch_mask: Optional[torch.Tensor] = None) -> Union[torch.Tensor, List[torch.Tensor]]:
"""
Forward pass of the NestedLinear layer.
Args:
x (torch.Tensor): Input tensor of shape (num_groups, num_experts, expert_capacity, hidden_dim).
dispatch_mask (Optional[torch.Tensor]): Dispatch mask for combining expert outputs.
Returns:
Union[torch.Tensor, List[torch.Tensor]]: Output tensor or list of tensors.
"""
assert len(x.shape) == 4, "Input must have 4 dimensions."
assert x.shape[1] == self.num_experts, "Number of experts must be the same."
num_groups, num_experts, expert_capacity, hidden_dim = x.shape
x_out = []
for i in range(num_experts):
dim_slice = hidden_dim // pow(2, i)
if self.nested_forward:
x_out.append(F.linear(x[:, i, :, :dim_slice], self.weight[:, :dim_slice], self.bias))
else:
x_out.append(F.linear(x[:, i], self.weight[:dim_slice, :], self.bias[:dim_slice] if self.bias is not None else None))
if self.combine_output and self.nested_forward and dispatch_mask is not None:
x_out = torch.stack(x_out, dim=1)
return torch.einsum('gec...,gtec->gt...', x_out, dispatch_mask)
else:
return x_outYou can view my full implementation here to find the code for the attention and feedforward layers. For the sake of brevity I will include the attention block below. As noted earlier this code resembles the standard attention block in a transformer. In this code we have integrated a router which chooses which experts are involved in computation. The attention and feedforward layers use linear layers to project a fraction of the hidden dimension of selected tokens to the model’s embedding dimension. We have to be careful of the shape of intermediate tensors which may have different dimensions for each expert. In the case of residual connections we pad them back to the embedding dimension and sum them appropriately as discussed in the paper. All tokens are combined using a weighted sum with the combine array.
class NestedBlock(nn.Module):
"""
Nested block combining attention and feed-forward layers.
Args:
embed_dim (int): Embedding dimension.
num_heads (int): Number of attention heads.
num_experts (int): Number of experts.
capacity_factor (Tuple[float, ...]): Capacity factors for each expert.
router_bias (bool): Whether to use router bias. Default: False.
jitter_noise (float): Jitter noise value. Default: 0.0.
"""
def __init__(
self,
embed_dim: int,
num_heads: int,
num_experts: int,
capacity_factor: Tuple[float, ...],
router_bias: bool = False,
jitter_noise: float = 0.0
):
super().__init__()
self.embed_dim = embed_dim
self.num_heads = num_heads
self.num_experts = num_experts
self.capacity_factor = capacity_factor
self.router = ExpertsPreferredMaskedRouter(
router_weights=RouterWeights(
embed_dim,
num_experts,
bias=router_bias
),
jitter_noise=jitter_noise
)
self.attention = NestedAttention(
embed_dim,
num_heads,
num_experts,
router_bias,
jitter_noise
)
self.feed_forward = NestedFeedForward(embed_dim, num_experts)
def forward(self, x: torch.Tensor, attn_mask: torch.Tensor, alpha: torch.Tensor) -> torch.Tensor:
"""
Forward pass of the NestedBlock.
Args:
x (torch.Tensor): Input tensor of shape (num_groups, num_tokens, embed_dim).
attn_mask (torch.Tensor): Attention mask.
Returns:
torch.Tensor: Output tensor of shape (num_groups, tokens_per_group, embed_dim).
"""
num_groups, num_tokens, embed_dim = x.shape
router_mask: RouterMask = self.router(
x,
calculate_capacity(self.capacity_factor, num_tokens)
)
x_experts = dispatch_to_experts(x, router_mask)
x_attn = self.attention(x_experts, router_mask, attn_mask)
x_attn = apply_residual(x_attn, x_experts)
x_ff = self.feed_forward(x_attn)
x_ff = apply_residual(x_ff, x_attn)
return combine_experts(x_ff, router_mask, alpha)